Counting Linear Extensions: GSoC Project Overview

I have been selected as a student developer in Google Summer of Code under the GeomScale organization & will be spending the upcoming 10 Weeks working on the project of “Counting Linear Extensions”. This post will be for providing details regarding my project, mainly problem formulation and proposed solution.

+

Project link

About the Organization

From the webpage of the organization:

“GeomScale is a research and development project that delivers open source code for state-of-the-art algorithms at the intersection of data science, optimization, geometric, and statistical computing”.

I have always been interested in the field of applied maths and this project immediately caught my attention. Currently, the organization works on mainly two open-source libraries, one of which is volesti, which is a C++ library with R and python interfaces, this library contains several algorithms for high-dimensional sampling and volume approximation. The other one is the recently introduced dingo, which is a python package for analyzing metabolic networks.

Introduction to my project

In brief, my project is to extend the functionality of the volesti library, in particular, implementing the functionality of “Counting Linear Extensions of a poset (partially ordered set)”. This problem can be converted to computing volume of a convex polytope, for which volesti contains state-of-the-art algorithms.

Exact problem description is as following:

The problem of counting the linear extensions of a given partial order consists of finding (counting) all the possible ways that we can extend the partial order to a total order that preserves the original partial order. It is an important problem with various applications in Artificial Intelligence and Machine Learning, for example in partial-order plans and in learning graphical models. It is a well known #P-complete problem; the fastest known algorithms are based on dynamic programming and require exponential time and space. Nevertheless, if we only need an approximate counting attained with a probability of success, then the problem admits a polynomial-time solution for all posets using Markov chain Monte Carlo (MCMC) methods. This project aims to implement new randomized methods to approximate the number of linear extensions based on volume approximation.

Mathematical details of the project

First, I will start by introducing the terms used in the above section, because once all the terms are clear, the aim of the project will become crystal clear (hopefully).

Poset

The term “poset” is short for “partially ordered set”, that is, a set whose elements are ordered but not all pairs of elements are required to be comparable in the order.

I will try to explain with an example: Let’s say you have marks of n=5 students in two exams, the marks of a student (out of 10) is given as a pair, let the marks of the students be as follows:

student-id	marks
$S_1$	(5, 8)
$S_2$	(7, 4)
$S_3$	(8, 3)
$S_4$	(9, 4)
$S_5$	(4, 2)

Now, let’s say your task is to find the topper of the class (yup, as always, creating an unnecessary competition in a learning environment). Now, there may exist many personal opinions on how to rank them, like take the sum (or mean) of two score, take the minimum of two scores etc. But, all these are subjective and can not be generalized to any pair of exams. The main point is that there exist a pair of students, which cannot be compared. for ex. $S_1$ and $S_3$ cannot be compared, similarly $S_1$ and $S_2$ cannot be compared, but there are some pairs which can be compared, like $S_1$ and $S_5$, as $S_1$ scored higher marks in both the subjects.

There exists many such examples, for ex. when you are deciding which laptop to buy, you may consider several features for comparing them, like: price, RAM size, screen size, processor, company etc.

• For representing the order between elements, we use the $\leq$ symbol (seems intuitive), so we can say that $S_5 \leq S_1$, $S_3 \leq S_4$ and so on.
• We say that elements $a, b$ of a poset are comparable, if either $a \leq b$ or $b \leq a$.
• Although the symbol is of $\leq$, but the binary relation can be of any sort, formally, a partial order is any binary relation that is reflexive (each element is comparable to itself), antisymmetric (no two different elements precede each other), and transitive. Complete definition can be obtained here

Representing poset as a Directed Acyclic Graph (DAG)

One graphical way of representing the poset is by using a directed graph.
This is done by representing each element of the poset by a node and there will be a directed edge between every pair of nodes $a \rightarrow b$ for which $a \leq b$.

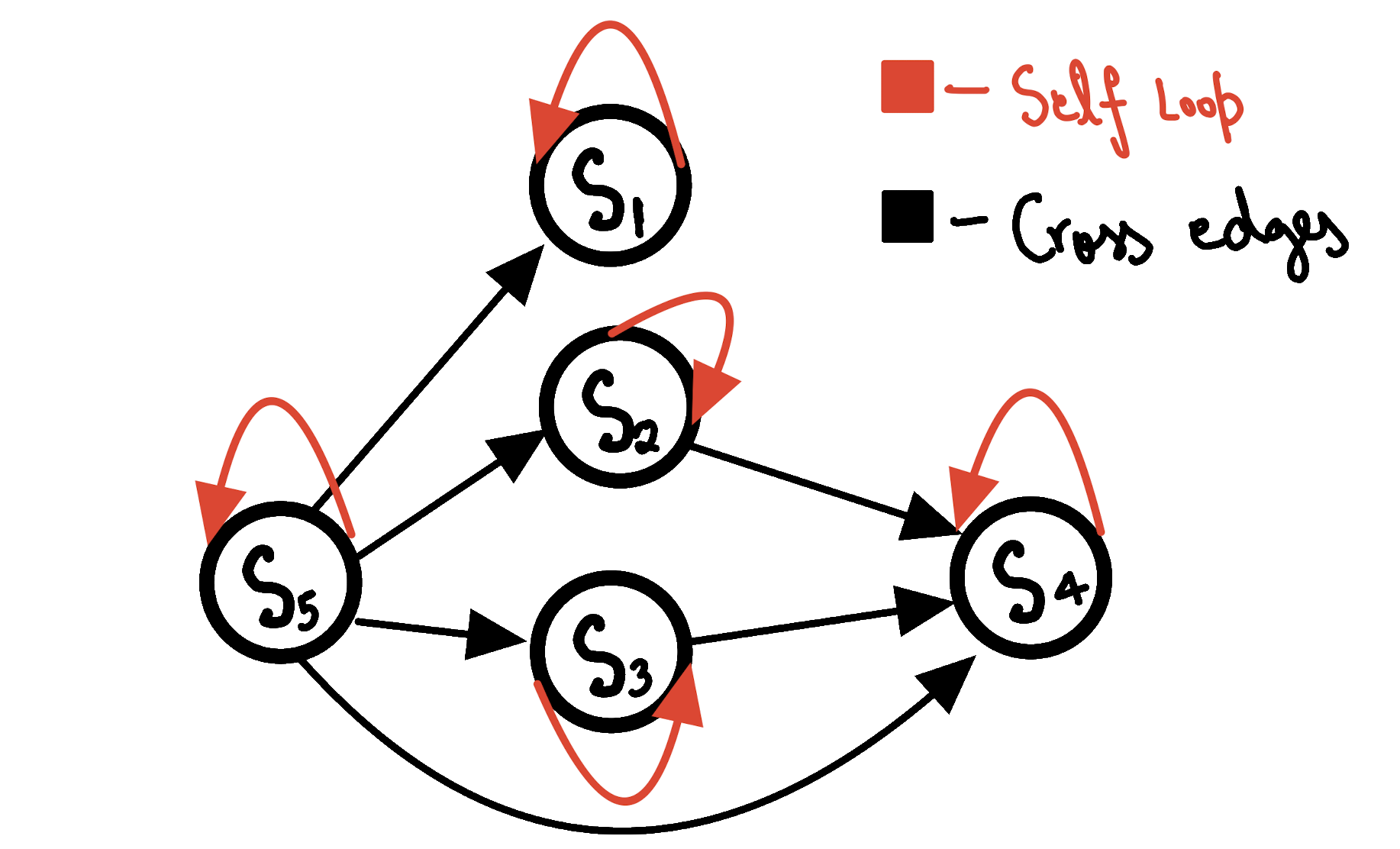
Directed (not yet acyclic) Graph representing the example poset

As can be easily seen in the above graph, it is not yet acyclic because of the self loops.
This can be solved easily, as we know that for every element $a$ in the poset, $a \leq a$ will always be true, hence we can simply remove the self loops for a more compact representation.
This results in the following graph:

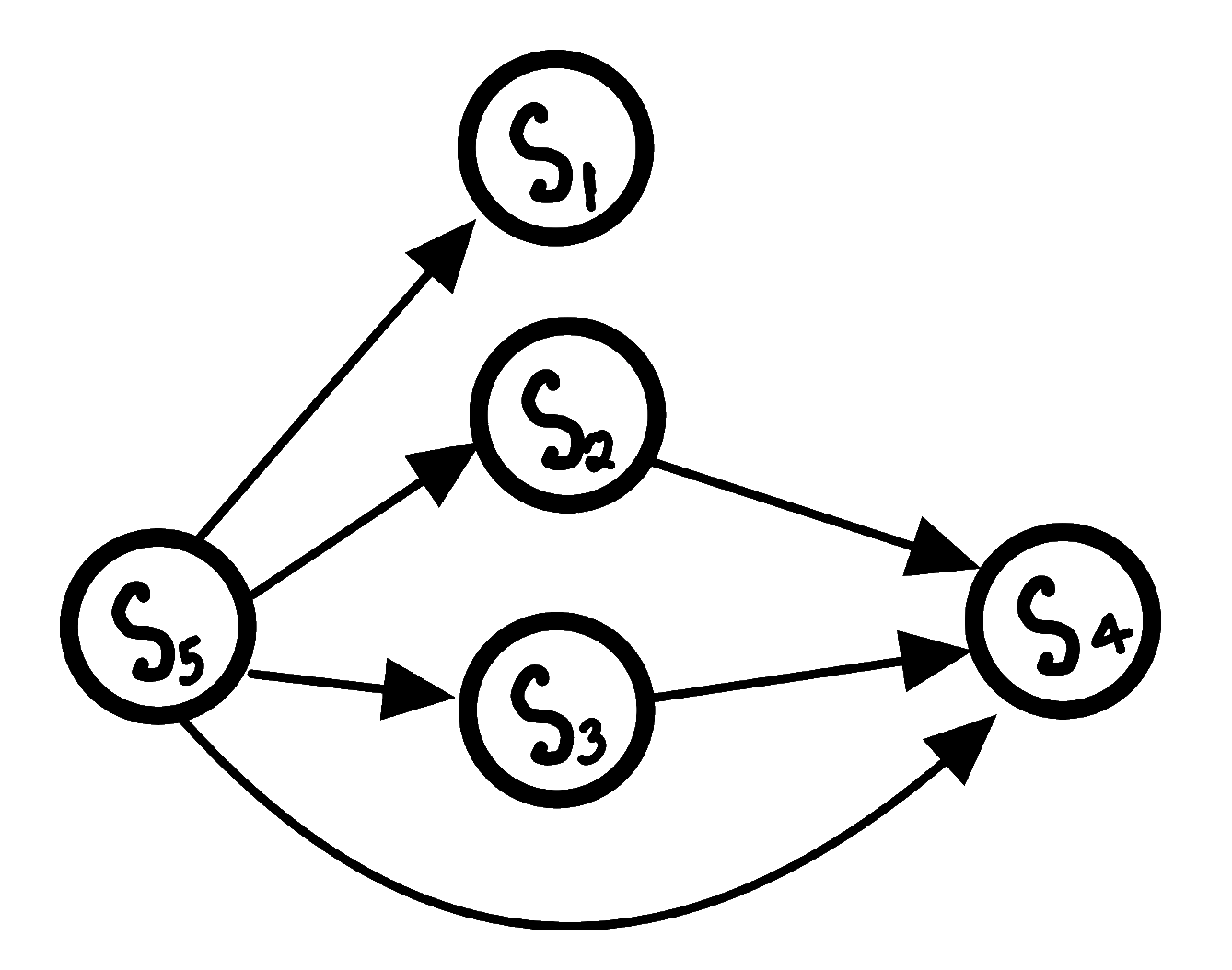
DAG representation of the example poset

Now, although the above graph is already a DAG, but if you observe carefully, it can be made even more compact.
This can be done by utilizing the transitive property of the partial order relations, i.e

$$ a \leq b, b \leq c \Rightarrow a \leq c $$

This means that in the above graph, when there is already an edge from $S_5 \rightarrow S_3$ and then $S_3 \rightarrow S_4$, then the edge $S_5 \rightarrow S_4$ is not giving us any extra information, this means it is implicit and can be removed.
This is known as finding the transitive reduction of a DAG, you can read more about it from here.

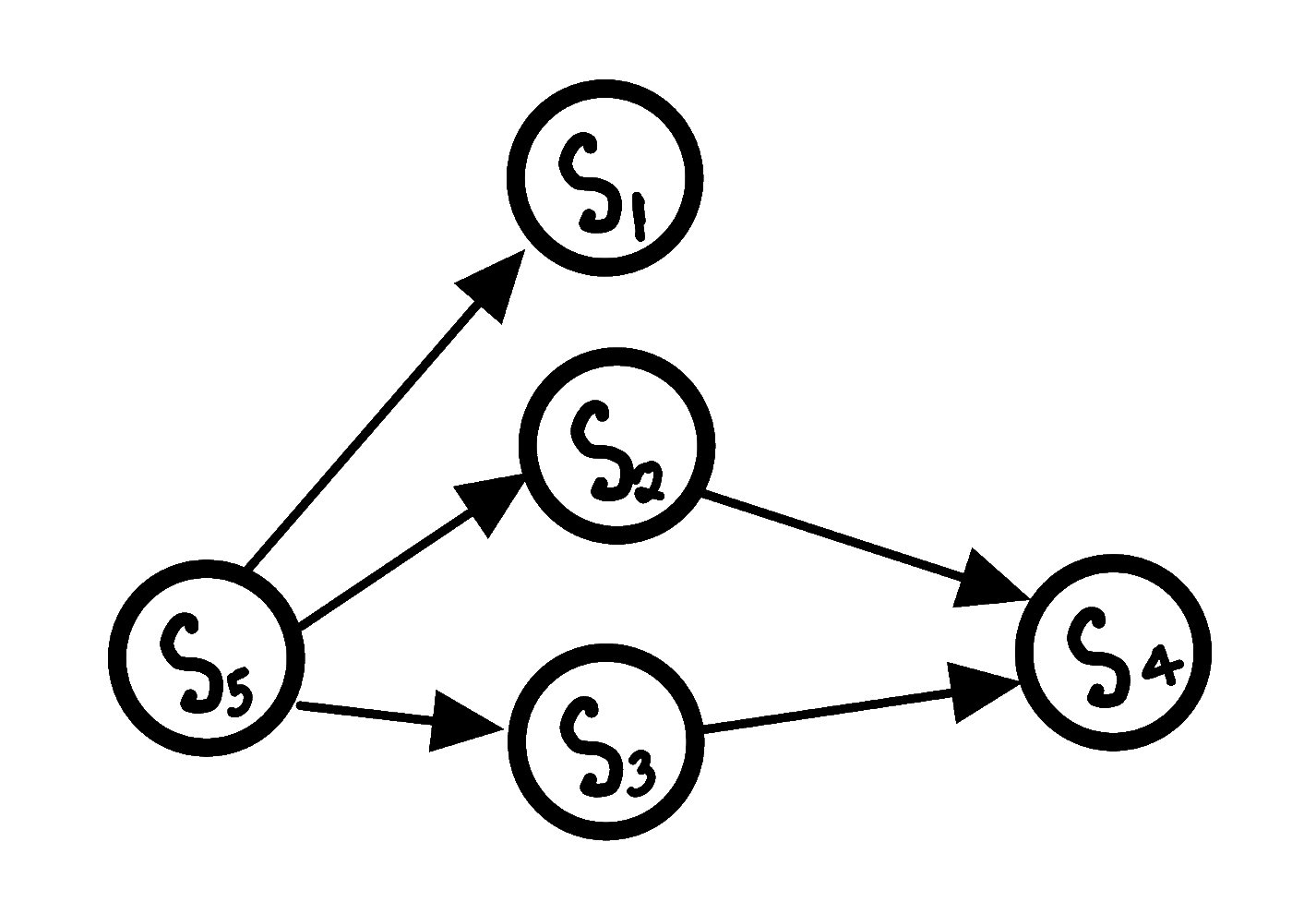
Transitive Reduction of the above DAG

Linear extensions of a poset

Let’s say we want to assign ranks to the students in our example, but didn’t we just discuss that there is ambiguity in that ??

Still, let’s say we have received a strict order from the principal of this school to assign ranks to the students, now you being a teacher with good ethics decides to assign ranks with a condition, if a student $b$ has better marks than student $a$ in both exams, i.e $a \leq b$ in the poset of the students, then definitely $b$ will get a better rank than $a$.

The following are 2 example rankings that you can assign to the students (the rightmost being rank 1 and leftmost being rank 5):

$$ \begin{align} & S_5 \leq S_2 \leq S_3 \leq S_4 \leq S_1 \newline & S_5 \leq S_1 \leq S_3 \leq S_2 \leq S_4 \end{align} $$

The above example rankings are examples of a total order, the only additional property of a “total order or a linear order” compared to a “partial order” is that any two elements are comparable.

Finally coming to definition of a linear extension:

A linear extension of a partial order is a total order or a linear order that is compatible with the partial order.

In the above definition, compatible means that if $a \leq b$ in the partial order, $\Rightarrow a \leq b$ in the extended total order.

A genuine question that may arise in your mind , what is so linear about it? Hint: think about how will the DAG representation of a totally ordered set look like after transitive reduction.

For fun: Prove that the number of linear extensions of a poset is equal to the number of topological orderings of it’s corresponding DAG.

Naive recursive algorithm for Counting Linear Extensions

Now that we know what a linear extension is, let’s devise a basic algorithm for counting the exact number of linear extensions.

• Even before thinking about an algorithm, let’s think about the scale of this number? For this, let’s take the worst case example, i.e a set of $n$ elements with no order between any pair of elements, it is easy to see that there are $n!$ number of linear extensions for this set. Thus, we see that the count of linear extensions can be very high ($n! \propto \sqrt{n} \left(\frac{n}{e}\right)^n$).

One way can be to enumerate all possible linear extensions, we gain insights from the above example of ranking the students, the high level view of the algorithm can be described as follows:

High level algorithm: Enumerate over all elements which can be ranked at the last of the $n$ elements, these are called minimal elements of the poset, nodes that are not greater than any other element of the poset, i.e a node $s$ is a minimal element if $\nexists$ any element $m$ s.t $m \leq s$. For each minimal element, place it at the end and then recurse for the remaining $n-1$ elements.

• The above algorithm is essentially enumerating over all possible linear extensions, so it’s time complexity will be $O(n!)$. Although, we can use memoization to avoid recomputing the subproblems (or use dynamic programming for bottom up approach), still the number of subproblems will be exponential in the worst case $\Big[ {n\choose 1} + {n\choose 2} + \dots = O(2^n) \Big]$.
• Although, the above algorithm is exponential, but the problem of Counting Linear Extensions is in fact #P-complete, i.e it is in #P and atleast as hard as all other problems in the time complexity class #P. (#P complexity class contains the counting versions of all the decision problems in the NP complexity class)

$$ \begin{align} \text{COUNT-LIN-EXT}(P) &= \sum_{x \in min(P)} \text{COUNT-LIN-EXT}(P \setminus x), \newline \text{where } min(P) & \text{ is the set of minimal elements of the poset P} \newline \end{align} $$

Geometric Interpretation

For a geometrical representation of our problem, we will consider an n-element poset in n-dimensional space. Also, to make the representation bounded, we will restrict the space inside the unit cube ([0,1]ⁿ).
The order relations can be interpreted as half spaces, thus the object formed has flat sides, hence it is a polytope (essentially an extension of polygons in high dimensions).
This special type of polytope formed for representing a poset is called an order-polytope.

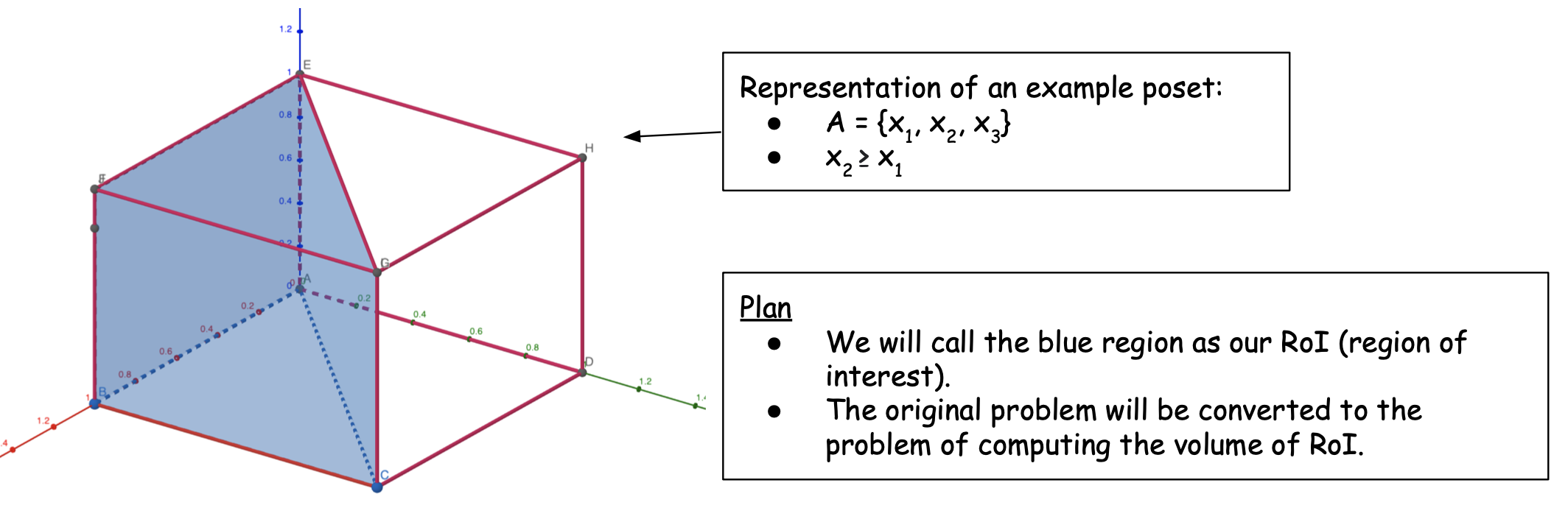
Geometric interpretation of an example poset as an order polytope.

Relation to volume computation

The following results will make a beautiful connection between counting linear extensions of a poset to the volume of its corresponding order polytope.

• RoI(P) = Union of all linear extensions of P
  • $\{x_1, x_2, x_3 \mid x_2 \leq x_3\} = \{x_1 \leq x_2 \leq x_3\} \cup \{x_2 \leq x_1 \leq x_3\} \cup \{x_2 \leq x_3 \leq x_1\}$.
• $Volume (RoI (P))$ = Sum of volumes of Linear Extensions of P
  • using the above the result and the fact that intersection of two linear extensions will have zero volume.
• Volume of every linear extension of P = $\frac{1}{n!}$ ; $n = $ number of elements (3 in the example)
  • can be seen by taking P = set with no relations in the second result and using symmetry.
• $Volume (RoI (P)) \times\ n!$ = Number of linear extensions of P
  • by combining the second and third result.

We have converted our problem of counting linear extensions into the problem of computing volume of polytopes in high dimensions.
As already stated, the problem of counting linear extensions is provably hard, and the above problem reduction takes polynomial time, this means that the problem of computing volume of polytopes in high dimensions is also provably hard.

(approximate) Volume computation in high dimensions

This is where GeomScale’s volesti library comes in - it contains implementations for efficiently approximating volumes of high dimensional convex objects, it does so by utilizing Multiphase Markov Chain Monte Carlo (MCMC) methods. You can read more about it from the documentations and paper mentioned in their README.

The images below provides a high level overview of these techniques:

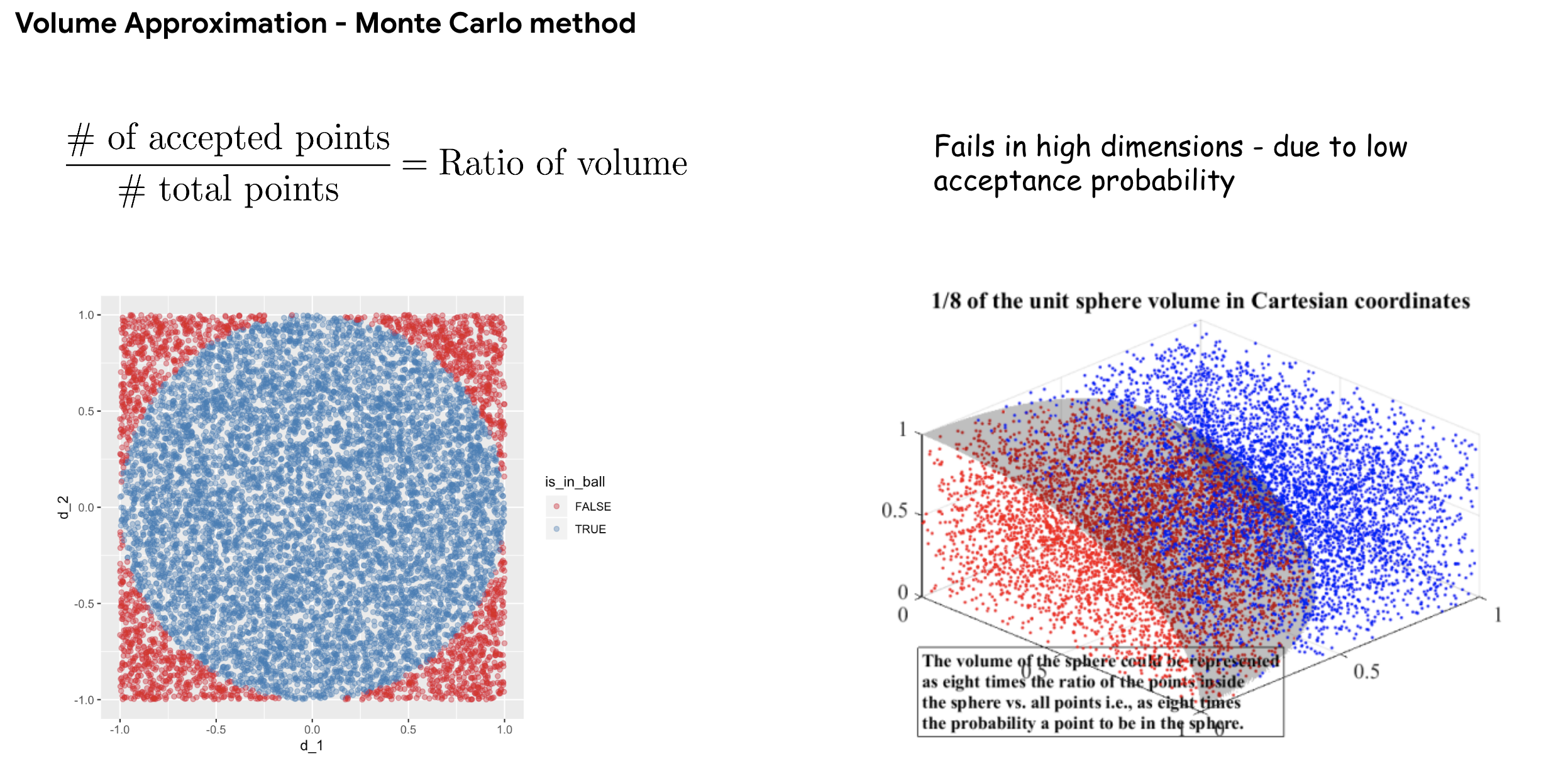
Monte Carlo method.

Multiphase Monte Carlo.

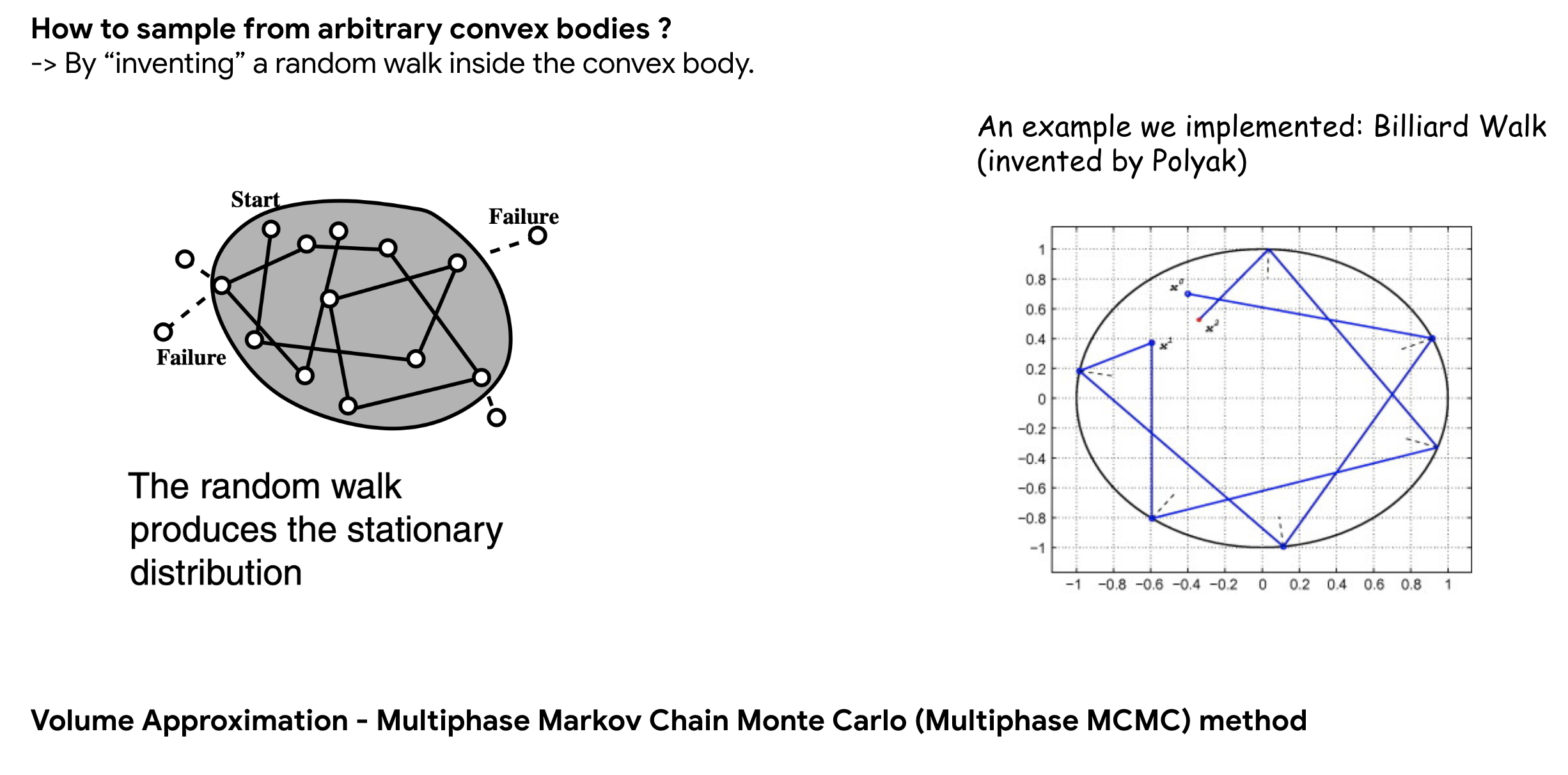
Markov Chain Monte Carlo.